交叉熵
交叉熵(cross entropy)是深度学习中常用的一个概念,一般用来求目标与预测值之间的差距。
信息论
1 信息量
信息量小:概率大的事件发生了。
信息量大:概率小的事件发生了。
越不可能的事件发生时,我们获取到的信息量就越大。越可能发生的事件发生了,我们获取到的信息量就越小。
假设X是一个离散型随机变量,概率分布函数为 Pr(X=x)=p(x),则定义事件X=x0的信息量为:
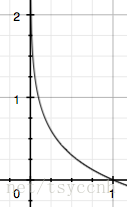
p(x)取值范围[0,1],信息量图:
横坐标为概率p,纵坐标为信息量 I。概率越小,信息量越大,概率越大,信息量越小。
2 熵
对于某个事件,有n种可能性,每一种可能性都有一个概率p(xi),可以计算出每个可能性的信息量,比如按下电脑开关的三种可能性:
| 序号 | 事件 | 概率p | 信息量I |
|---|---|---|---|
| A | 电脑正常开机 | 0.7 | -log(p(A))=0.36 |
| B | 电脑无法开机 | 0.2 | -log(p(B))=1.61 |
| C | 电脑爆炸了 | 0.1 | -log(p(C))=2.30 |
熵表示所有信息量的期望,定义熵为:
其实就是以每个可能性的概率为权重,对信息量做加权求和。
所以上面电脑开机问题的熵为
此外还有一类比较特殊的问题,比如投掷硬币只有两种可能,我们称之为0-1分布问题(二项分布的特例),对于这类问题,熵的计算方法可以简化为如下算式:
3 相对熵(KL散度)
KL 散度用来衡量两个单独的概率分布 P(x) 和 Q(x)的差异,即如果用 P 来描述目标问题,而不是用 Q 来描述目标问题,得到的信息增量。
在机器学习中,用 P 来表示样本的真实分布,比如[1,0,0]表示当前样本属于第一类。用 Q 来表示模型所预测的分布,比如[0.7,0.2,0.1]。
用 Q 来描述样本,虽然可以大致描述,但是信息量不足,需要额外的一些“信息增量”才能达到和 P 一样完美的描述。模型训练就是为了降低这个所需的“信息增量”。如果我们的Q通过反复训练,直到不再需要额外的“信息增量”也能完美的描述样本,此时Q等价于P。
KL散度的计算公式:
KL散度值越小,表示P分布和Q分布越接近。
4 交叉熵
KL散度公式拆开:
等式的前一部分恰巧就是p的熵的相反数,等式的后一部分,就是交叉熵:
在机器学习中,我们需要评估label和predicts之间的差距,原本应该是使用KL散度的,但是由于KL散度中的前一部分 −H(p(x)) 只与真实label有关,是固定不变的,故在优化过程中,只需要关注交叉熵就可以了。所以一般在机器学习中直接用用交叉熵做loss,评估模型。
机器学习中交叉熵的应用
1 交叉熵在单分类问题中的使用
单分类问题,每一张图像样本只能有一个类别,交叉熵在单分类问题上基本是标配的loss function
比如一个样本的label和预测概率分布:
| * | 猫 | 青蛙 | 老鼠 |
|---|---|---|---|
| Label | 0 | 1 | 0 |
| Pred | 0.3 | 0.6 | 0.1 |
单分类的Pred是用softmax算出来的,各个类别的概率之和为1
此样本的交叉熵计算过程如下:
一个batch的loss则是每个sample的交叉熵loss平均值。
2 交叉熵在多分类问题中的使用
多分类问题,每一张图像样本可以同时有多个类别。单分类问题的标签为one-hot,多分类的标签是n-hot。
比如一个样本的label和预测概率分布:
| * | 猫 | 青蛙 | 老鼠 |
|---|---|---|---|
| Label | 0 | 1 | 1 |
| Pred | 0.1 | 0.7 | 0.8 |
多分类的Pred是用sigmoid算出来的,每个类别概率独立分布,交叉熵在这里是单独对每一个节点进行计算,每一个节点只有两种可能值,所以是一个二项分布。前面说过对于二项分布这种特殊的分布,熵的计算可以进行简化。同样的,交叉熵的计算也可以简化:
此样本的交叉熵计算过程如下:
同样,一个batch的loss则是每个sample的交叉熵loss平均值。
 冯aba林
冯aba林